When it comes to numbers, few things are as satisfying as the simplicity of exponents. Take “2 to the 3rd power,” for instance. It’s not just a math problem; it’s a gateway to understanding the magic of multiplication in a whole new light. Picture this: you’ve got two friends, and each of them brings two more friends to the party. Before you know it, you’ve got a whole crowd!
Table of Contents
ToggleUnderstanding Exponents
Exponents simplify expressions involving repeated multiplication. They represent how many times a number, called the base, is multiplied by itself.
Definition of Exponents
An exponent consists of a base and a superscript numeral. The base indicates the number to multiply, while the exponent signifies the number of times to perform that multiplication. For instance, in “2 to the 3rd power,” 2 is the base, and 3 is the exponent. This notation provides a concise way to express complex calculations. Understanding exponents reveals their utility in areas like algebra and scientific notation, where they represent large or small values efficiently.
Basic Rules of Exponents
Several fundamental rules govern the use of exponents. First, multiplying two numbers with the same base entails adding their exponents. For example, (2^3 times 2^2) equates to (2^{3+2}) or (2^5). Next, dividing numbers with the same base requires subtracting the exponents. In this case, (2^5 ÷ 2^3) simplifies to (2^{5-3}), resulting in (2^2). Raising a power to a power means multiplying the exponents, where ((2^3)^2) leads to (2^{3 times 2}) or (2^6). Following these rules streamlines computation and enhances understanding of exponential functions.
Calculating 2 to the 3rd Power
Calculating 2 to the 3rd power involves a straightforward approach. Start with the base, which is 2. Multiply it by itself three times. The process looks like this:
- First, multiply 2 by 2 to get 4.
- Next, multiply 4 by 2, resulting in 8.
The final result shows that 2 to the 3rd power equals 8. This calculation illustrates how exponents simplify repeated multiplication.
Step-by-Step Calculation
Step through the multiplication for clarity. Begin with the first multiplication.
- Take 2 and multiply by 2, which gives 4.
- Follow that by multiplying 4 by 2 to arrive at 8.
2 to the 3rd power specifically means multiplying 2 by itself three times. That promotes a clear understanding of exponentiation.
Visual Representation of the Calculation
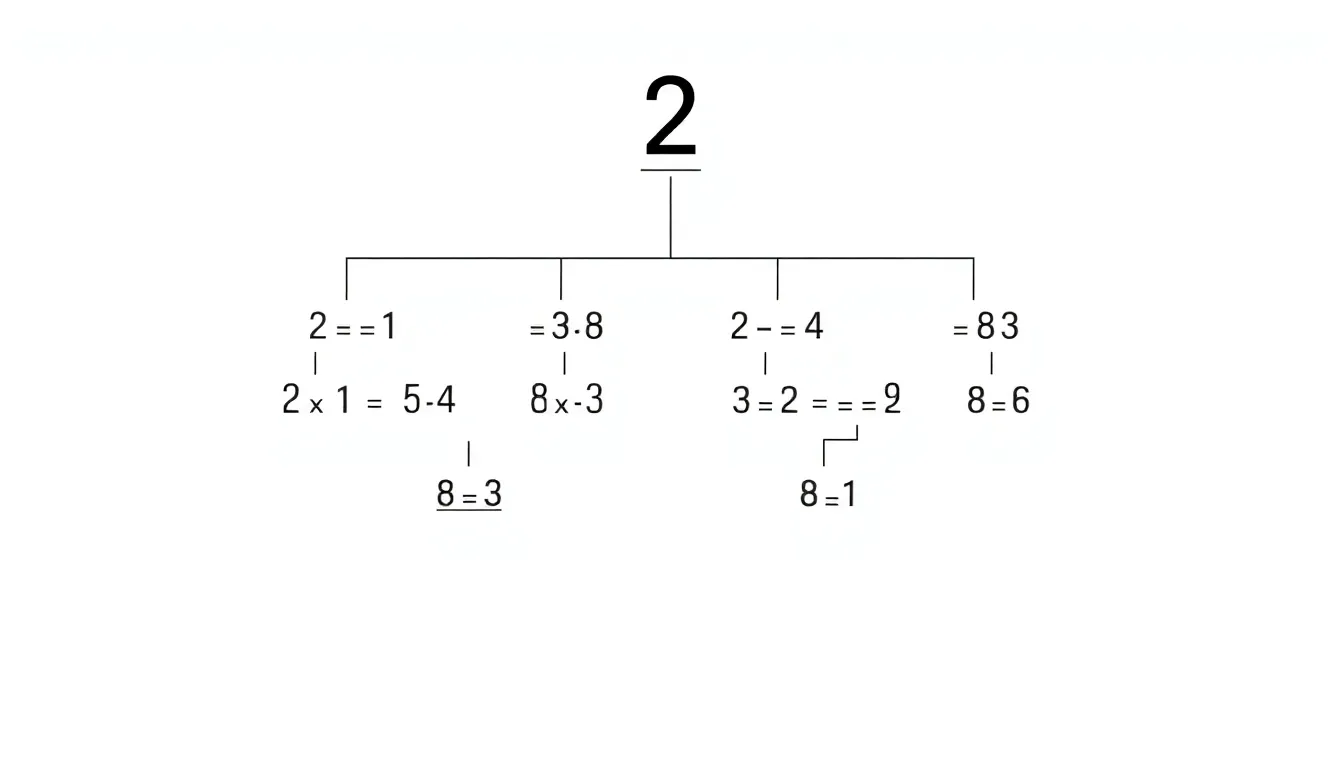
Visual aids enhance comprehension of calculations. A tree diagram effectively illustrates how each multiplication branches out.
- At the top, start with the base number, 2.
- Draw two lines from that point, each leading to another 2, representing the first multiplication.
- Continue the branches to illustrate the final multiplication from 4 to 8.
This representation provides a clear visual of the steps involved in calculating 2 to the 3rd power. Seeing the multiplication process visually reinforces the concept of exponents.
Applications of 2 to the 3rd Power
Two to the 3rd power, equating to 8, has various practical applications in everyday scenarios.
Real-World Examples
In everyday life, 2 to the 3rd power serves in calculating amounts. For instance, when organizing a party, if each person brings 2 additional friends, the total rapidly escalates. This sort of exponential growth illustrates how quickly a group can expand. Similarly, in the context of a square, each side measuring 2 units results in an area of 8 square units, showcasing its relevance in geometry. Additionally, doubling ingredients in recipes highlights the convenience of using exponential notation. Applying 2 to the 3rd power simplifies many calculations, emphasizing its utility.
Importance in Computer Science
Computer science greatly values 2 to the 3rd power due to its connection to binary systems. In binary, each bit represents a power of 2. Thus, 2 to the 3rd power indicates processing 8 distinct values. Data structures, such as binary trees, utilize this concept to optimize storage and retrieval operations. Enhancements in algorithms often relate directly to exponents, influencing efficiency in calculations. Additionally, memory addressing frequently operates on powers of 2, making this understanding crucial for software development. System designs leverage this principle to maximize performance and functionality across various applications.
Related Concepts in Mathematics
Exponents link to several essential mathematical concepts, such as powers, roots, and binary numbers. Understanding these connections deepens comprehension of exponentiation.
Powers and Roots
Powers represent repeated multiplication. For instance, calculating (2^3) involves multiplying 2 by itself three times. Roots, on the other hand, indicate the inverse operation. For example, the square root of 4 asks what number, when raised to the power of 2, equals 4. This connection between powers and roots allows efficiency in simplifying expressions. Simplified calculations involve recognizing that raising a number to a power and taking its root provides quick ways to arrive at solutions.
Relationship to Binary Numbers
Binary numbers utilize powers of two extensively. Each digit in binary, or a bit, signifies a power of 2. Starting from the right, the first bit represents (2^0), the second (2^1), and so forth. This system underpins how computers process data. For instance, the binary number 110 represents (1 times 2^2 + 1 times 2^1 + 0 times 2^0), equating to 6 in the decimal system. This relationship highlights the significance of exponentiation in tech, especially in algorithms and data structures that rely on binary representation for efficient computation.
Understanding “2 to the 3rd power” opens the door to grasping the broader implications of exponents in mathematics and real-world applications. This simple yet powerful concept not only simplifies calculations but also enhances comprehension in various fields. From organizing events to optimizing data structures in computer science, the relevance of exponentiation is undeniable. As individuals continue to explore mathematical principles, recognizing the significance of exponents will undoubtedly enrich their analytical skills and problem-solving abilities. Embracing this knowledge fosters a deeper appreciation for the interconnectedness of mathematics and technology in everyday life.

